Let us study a somewhat more complex case of motion in a gravitational field. Instead of just the force of gravity, let us add a
drag force which is proportional to the velocity, that is: $$ {\bf F} = - \alpha {\bf v}. $$ In other words, at every instant, the drag force is proportional to the velocity and has an opposite direction. The constant of proportionality α includes all the physics of the flow around the object, and for us, it is simply assumed to be given.
Just for general knowledge, such a drag law does exist. It describes the drag on objects moving in a very
viscous fluid, such as a marble droped through honey. In such a case, the parameter α will depend on the size of the marble and the viscosity of the honey (the actual dependence is beyond the scope of this course, if you're curious though, it is linear in the radius and the viscosity, as is explained
here). In less viscous cases, such as a marble dropped through air, the drag force typically grows like the velocity to a higher power (usually close to 2). But this we will leave for the example below!
Back to our problem. If the only forces are that of gravity and drag, the second law of motion would imply that: $$ m {d{\bf v} \over dt} = {\bf F}_g + {\bf F}_d = m {\bf g} - \alpha {\bf v} $$ How does this equation behave?
To answer this question, we will try to understand the behavior before we actually solve the equation.
First, in the limit of small velocities, we find that the drag which of course is proportional to the velocity, is small as well, and can therefore be neglected. Once this is done, we find the trivial case of free fall:
$$ \require{cancel}
m {d{\bf v} \over dt} = {\bf F}_g + \cancelto{0}{{\bf {F}}_d} \approx m {\bf g} ~~\Rightarrow~~v\approx g t $$ (again, we define the positive direction to be down, hence the velocity increases).
For large velocities, we expect the acceleration term to dissapear, giving a balanced gravitational and drag forces, from which we can derive the asymptotic velocity:
$$ \require{cancel} \cancelto{0} {m {d{\bf {v}} \over dt}}
\approx {\bf F}_g + {\bf F}_d = m {\bf g} - \alpha{\bf v} ~~\Rightarrow~~v_{\infty} = {m g \over \alpha}. $$
From the two limiting behaviors, we can draw a heuristic graph, as can be seen in the figure.
Now that we understand the behavior of the falling object, we can solve for the actual motion. If we take the z component of eq. (1) above (i.e., take the scalar product $\cdot {\hat{\bf z}}$ on both sides, we get the scalar equation: $$ m { dv_z \over dt} = m g - \alpha v_z .$$
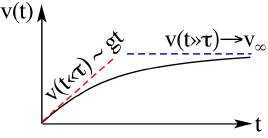
The velocity as a function of time. For small t's, the velocity is small, the drag is therefore negligible and the motion is that of free fall. Hence, v grows linearly. For large t's, the velocity approaches its asymptotic value, where the drag equals gravity.
This equation is a
differential equation because it relates a variable, v
z, to its derivatives (in this case, to its first derivative dv
z/dt). How do we solve such an equation? Well, the truth is that solving differential equations is an art. There is no recipe to solve all differential equations just as there is no recipe to solve all integrals. Each differential equation, just like every integral, requires knowing how to solve that particular type, or how to transform it to a form for which a solution is known.
This type of equation can be solved through
separation of variables. See inset below for how they are generally solved. It is one of two types of equations which we will solve in this course.
In our case, we separate the t's and dt's to one side, and the v
z's and dv
z's to the other side. We obtain: $$ m { dv_z \over m g - \alpha v_z} = dt .$$ What this equation implies is that for any infinitesimally small time step dt, there will be the same change in the velocity dv
z times the paritular function of v
z. To get the actual v
z(t), we will have to integrate over many of those changes, over time on one hand, and over dv
z on the other. We omit the "z" for brievety: $$ \int_{v=0}^{v(t)} {m dv \over m g - \alpha v} = \int_{t=t_0}^{t} dt .$$