Passing the Eddington limit without getting a ticket (cont.)
-- back to page 1 --
Recent quantitative stability analyses by Shaviv (2001a) do lead to the conclusion that even the simple case of a pure “Thomson atmosphere”—i.e., one with only Thomson scattering of radiation by free electrons—would be subject to intrinsic instabilities and develop lateral inhomogeneities. The analysis by Shaviv (2001a) suggests in particular that these instabilities share many similar properties to the excitation of strange mode pulsations (e.g., Glatzel 1994; Papaloizou et al. 1997). For example, both type of instabilities are favored when radiation pressure dominates over gas pressure. Both arise when the temperature perturbation term in the effective equation of state for the gas becomes non-local. In strange mode instabilities, the term arises because the temperature in the diffusion limit depends on the radial gradient of the opacity perturbations. In the lateral instability, the term depend on the lateral radiative flux which arises from non-radial structure on a scale of the vertical scale height.
Note that when conditions of a pure Thomson atmosphere are alleviated, more instabilities exist. There are of course the aforementioned strange mode instabilities which require a non-Thomson opacity. If magnetic fields are introduced, even more instabilities can play a role (Arons 1992; Gammie 1998; Begelman 2002; Blaes & Socrates 2003). We stress however that the physical origin of the instabilities is not important to our discussion here. The only critical point is that as atmospheres approach the Eddington limit, non-radial instabilities do exist to make the atmospheres inhomogeneous, while the typical length scale expected is that of the vertical scale height.
In the presence of inhomogeneities, the flux through the system can be written as the volume average of the flux: Favr = ⟨F⟩v, where ⟨ ⟩v is the volume weighted average. On the other hand, the force exerted by this flux is favr = ⟨F κv⟩v, thus, an effective opacity can be defined as (Shaviv 1998): $$\kappa_{\mathrm{eff}} \equiv {f_{avr} \over F_{avr}} = {\langle F \kappa_V \rangle_V \over {\langle F\rangle_V}} .$$ The situation is very similar to the case where inhomogeneities are present in frequency space, i.e., in non-gray atmospheres. In such a case, the Rosseland mean will be used to calculate the radiative flux through the system, while the Force mean, which is the flux weighted opacity, is used for the force. The two cases are similar, with inhomogeneities in either frequency space or in real space.
For a few unique opacity laws, the effective opacity can increase. However, more generally, as is the special case of Thomson scattering, the effective opacity is reduced once any inhomogeneities are present.
One example where κeff can be calculated is the limit of small isotropic perturbations in the optically thick limit of a Thomson-scattering atmosphere having a negligible gas heat capacity such that ∇ ⋅ F = 0. This limit corresponds to the top layers of an atmosphere of a luminous object (yet deep enough for the inhomogeneities to remain opaque). In this case (Shaviv 1998), $$\kappa_{\mathrm{eff}} = \kappa_0 \left[ 1- \left( d-1 \over d\right) \sigma^2 \right], $$ where σ is the normalized standard deviation of ρ, and d is the dimension of the system. This result demonstrates that inhomogeneities reduce the effective opacity, but the reduction does not take place in a 1-D system. In other words, the porosity effect is intrinsically non-radial.
In Shaviv (2000) it was demonstrated that the main problem in obtaining a super-Eddington state is shifting the critical point, above which the atmosphere is unbound, upwards to where the density is lower. The existence of a porous layer can serve this role, the “missing link” between the top of the convection zone and the critical point where a wind initiates. It therefore allows the construction of a super-Eddington steady state, the main elements of which are the following:
The mass loss rate can then be obtained by identifying the sonic point of a steady state wind with the critical point, which is the radius where the radiative and gravitational forces balance each other. We then have M-dot = 4πR2 ρcritical vsonic. Furthermore, this can generally be reduced to the form of (Shaviv 2001b):
The mass loss predicted by the super-Eddington theory was compared with observations of super-Eddington objects which have good observational data. These were two novae which are not very fast and which have the best determined absolute bolometric evolution: FH-Ser and LMC 1988 #1. The theory was also applied to the Luminous Blue Variable star η-Car.
For the two novae, we find that the predicted mass loss rates agree with their observations if W ≈ 10 ± 5, which is clearly consistent with the theoretical estimate for W. The agreement is also with the temporal evolution of the velocities, if those are taken to be the primary absorption line component.
Using W ≈ 10±5, the mass loss equation can also be applied to η-Car, which is an entirely different object from novae (in mass, mass loss rate and duration, photospheric size etc). The predicted integrated mass loss is in agreement older determinations, of 1-2Msun of ejecta (e.g., Davidson & Humphreys 1997), while the terminal velocity is consistently predicted as well.
Recent observations of η-Car reveal a larger than previously estimated amount of ejected mass (Smith et al. 2003). If the inferred ejected mass is indeed as high as 10 Msun it could indicate that the clumps in the continuum driven winds have a power law scaling law. This was shown by Owocki et al. (2004) to lead a modified mass loss luminosity relation, with larger mass loss rates: $$ \dot{M} = {{W(\Gamma) L_\mathrm{Edd} (\Gamma - 1)^p \over c v_s} } $$ where the power p is related to the power law αp in the truncated distribution of “clump” optical depths: $$ \tau {d f \over d \tau} = {1 \over \Gamma [\alpha_p]} \left( \tau \over \tau_0 \right)^{\alpha_p} e^{-(\tau/\tau_0)} $$ with p = min(1, αp ). It can better explain the larger mass loss rates from η-Car.
 More quantitative tests of the theory are in progress, as is its application to other objects (such as Super-Massive Stars).
More quantitative tests of the theory are in progress, as is its application to other objects (such as Super-Massive Stars).
Links:
Back to page 1
Back to Personal Research
Back to Home page
The Technical Details
Instabilities of luminous atmospheres
We begin by pointing out that as atmospheres approach the Eddington limit, they become radiative-hydrodynamically unstable. This, as we show below, is crucial for the development of super-Eddington atmospheres. The hunch that such atmospheres may become unstable was already floating around for quite some time, since Spiegel (1976, 1977) speculated that atmospheres supported by radiation pressure would likely exhibit instabilities not unlike that of Rayleigh-Taylor, associated with the support of a heavy fluid by a lighter one, thus leading to formation of “photon bubbles”.Recent quantitative stability analyses by Shaviv (2001a) do lead to the conclusion that even the simple case of a pure “Thomson atmosphere”—i.e., one with only Thomson scattering of radiation by free electrons—would be subject to intrinsic instabilities and develop lateral inhomogeneities. The analysis by Shaviv (2001a) suggests in particular that these instabilities share many similar properties to the excitation of strange mode pulsations (e.g., Glatzel 1994; Papaloizou et al. 1997). For example, both type of instabilities are favored when radiation pressure dominates over gas pressure. Both arise when the temperature perturbation term in the effective equation of state for the gas becomes non-local. In strange mode instabilities, the term arises because the temperature in the diffusion limit depends on the radial gradient of the opacity perturbations. In the lateral instability, the term depend on the lateral radiative flux which arises from non-radial structure on a scale of the vertical scale height.
Note that when conditions of a pure Thomson atmosphere are alleviated, more instabilities exist. There are of course the aforementioned strange mode instabilities which require a non-Thomson opacity. If magnetic fields are introduced, even more instabilities can play a role (Arons 1992; Gammie 1998; Begelman 2002; Blaes & Socrates 2003). We stress however that the physical origin of the instabilities is not important to our discussion here. The only critical point is that as atmospheres approach the Eddington limit, non-radial instabilities do exist to make the atmospheres inhomogeneous, while the typical length scale expected is that of the vertical scale height.
Inhomogeneities and a reduced effective opacity
The next point to note is that once instabilities are excited in an atmosphere, the unstable modes will grow to become nonlinear. These inhomogeneities play an important role because, once introduced, they change the ratio between the radiative flux through the system and the radiative force.In the presence of inhomogeneities, the flux through the system can be written as the volume average of the flux: Favr = ⟨F⟩v, where ⟨ ⟩v is the volume weighted average. On the other hand, the force exerted by this flux is favr = ⟨F κv⟩v, thus, an effective opacity can be defined as (Shaviv 1998): $$\kappa_{\mathrm{eff}} \equiv {f_{avr} \over F_{avr}} = {\langle F \kappa_V \rangle_V \over {\langle F\rangle_V}} .$$ The situation is very similar to the case where inhomogeneities are present in frequency space, i.e., in non-gray atmospheres. In such a case, the Rosseland mean will be used to calculate the radiative flux through the system, while the Force mean, which is the flux weighted opacity, is used for the force. The two cases are similar, with inhomogeneities in either frequency space or in real space.
For a few unique opacity laws, the effective opacity can increase. However, more generally, as is the special case of Thomson scattering, the effective opacity is reduced once any inhomogeneities are present.
One example where κeff can be calculated is the limit of small isotropic perturbations in the optically thick limit of a Thomson-scattering atmosphere having a negligible gas heat capacity such that ∇ ⋅ F = 0. This limit corresponds to the top layers of an atmosphere of a luminous object (yet deep enough for the inhomogeneities to remain opaque). In this case (Shaviv 1998), $$\kappa_{\mathrm{eff}} = \kappa_0 \left[ 1- \left( d-1 \over d\right) \sigma^2 \right], $$ where σ is the normalized standard deviation of ρ, and d is the dimension of the system. This result demonstrates that inhomogeneities reduce the effective opacity, but the reduction does not take place in a 1-D system. In other words, the porosity effect is intrinsically non-radial.
The super-Eddington State
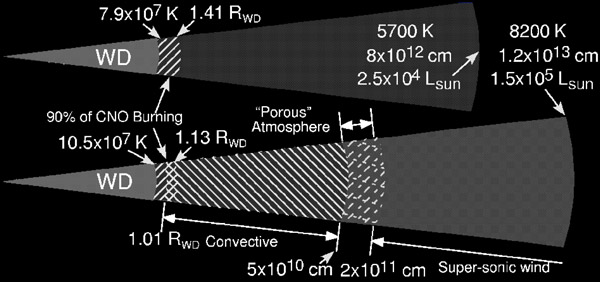
Joss et al. (1973) have shown that deep inside the star, convection will always be excited as the Eddington limit is approached. Convection, however, can only remain efficient as long as the density is high enough, such that the convection motion can carry enough of the flux to keep the leftover carried by radiation at a sub-Eddington level. Moreover, the most efficient convection is obtained when the internal convective motions approach sonic velocities. This allows us to calculate the density below which convection will fail to carry enough flux to keep the radiation field sub-Eddington. Below this density, the super-Eddington radiation field will drive a wind. This mass loss can be estimated to be: $$ \dot{M}_\mathrm{conv} \approx {L \over v_{s}^2} , $$ which is enormous. Super-Eddington objects should have evaporated on very short time scales, but they don't. To solve the existence problem of super-Eddington states, one therefore requires moving the critical point (the radius where the radiation pressure balances the gravitational pull) higher in the atmosphere to where the density (and ensuing mass loss) is much lower.In Shaviv (2000) it was demonstrated that the main problem in obtaining a super-Eddington state is shifting the critical point, above which the atmosphere is unbound, upwards to where the density is lower. The existence of a porous layer can serve this role, the “missing link” between the top of the convection zone and the critical point where a wind initiates. It therefore allows the construction of a super-Eddington steady state, the main elements of which are the following:
- Region A: Convection Zone. In the innermost region, where the density is sufficiently high any excess flux above the Eddington luminosity is necessarily advected through convection, which is always excited before the Eddington limit is reached (Joss et al., 1973). Therefore, the radiative luminosity remains in this region below the classical Eddington limit: Lrad < LEdd < Ltot.
- Region B: The porous atmosphere. Once the density decreases sufficiently, as one moves outwards, convection becomes inefficient. Instabilities will necessarily render the atmosphere inhomogeneous, thus facilitating the transfer of flux without exerting as much force. The effective Eddington luminosity is larger than the classical Eddington luminosity: LEdd < Lrad = Ltot < Leff. η-Car has shown us that the existence of this region allows for the steady state outflow during its 20 year long eruption (Shaviv, 2000).
- Region C: Optically Thick Wind. When perturbations arising from the instabilities, which are expected to be of order the atmospheric scale height, lose their opaqueness, the effective opacity tends to the microscopic value and the effective Eddington limit tends to the classical value. At the transition between regions (B) and (C), the effective Eddington luminoisty is equal to the total luminosity. This critical point is also the sonic point in a continuum driven steady-state wind. Above the transition surface, Ltot > Leff → LEdd and we have an optically thick super-sonic wind.
- Region D: Optically Thin Wind. At a large enough radius, the geometrical dilution makes the wind transparent. The boundary between the regions is the photosphere of the ob ject. Namely, it sits in the wind. The ob ject itself is obscured.

The Structure of a Nova according to the old lore (top) and according the new super-Eddington theory. According to the old picture, the steady state part of novae should be close to but less than Eddington and given by the classical core mass luminosity relation (Paczynski, 1970). In it, a degenerate core is surrounded by a hydrogen rich envelope which burns into Helium in a shell at its base (through the CNO cycle). If one allows the formation of a porous atmosphere a second solution is obtained. This solution is super-Eddington and has an optically thick wind. This wind is important because it determines the appearnce of the object and because the wind mass loss determines the evolution of the Nova (Shaviv, 2002).
Winds from super-Eddington Atmospheres
The atmosphere can remain effectively sub-Eddington while being classically super-Eddington, only as long as the inhomogeneities comprising the atmosphere are optically thick. Clearly however, this assumption should break at some point where the density is low enough. From that radius outwards, the radiative force overcomes the gravitational pull and a wind is generated.The mass loss rate can then be obtained by identifying the sonic point of a steady state wind with the critical point, which is the radius where the radiative and gravitational forces balance each other. We then have M-dot = 4πR2 ρcritical vsonic. Furthermore, this can generally be reduced to the form of (Shaviv 2001b):
$$ \dot{M} = {W(\Gamma) (L-L_\mathrm{Edd}) \over c v_s} , $$
where
W is a dimensionless wind “function”. In principle, W can be calculated
from first principles only after the nonlinear state of the inhomogeneities is fully
understood. This however is still lacking as it requires elaborate 3D numerical
simulations of the nonlinear steady state. Nevertheless, it can be done in several
phenomenological models which only depend on geometrical parameters such as
the average size of the inhomogeneities in units of the scale height
(β ≡ d/lp ),
the average ratio between the surface area and volume of the blobs in units of the
blob size (Ξ), and the volume filling factor α of the dense blobs. For example,
in the limit where the blobs are optically thick, one obtains that
$$ W = {3 \Xi \over 32}\sqrt{\nu} \alpha \beta (1-\alpha)^2 .$$
Here ν is the ratio between the effective and adiabatic speeds of sound. Thus,
W depends only on geometrical factors. It does not depend explicitly on the
Eddington parameter Γ. Typical values of
W ~ 1-10 are thus obtained. The mass loss predicted by the super-Eddington theory was compared with observations of super-Eddington objects which have good observational data. These were two novae which are not very fast and which have the best determined absolute bolometric evolution: FH-Ser and LMC 1988 #1. The theory was also applied to the Luminous Blue Variable star η-Car.
For the two novae, we find that the predicted mass loss rates agree with their observations if W ≈ 10 ± 5, which is clearly consistent with the theoretical estimate for W. The agreement is also with the temporal evolution of the velocities, if those are taken to be the primary absorption line component.
Using W ≈ 10±5, the mass loss equation can also be applied to η-Car, which is an entirely different object from novae (in mass, mass loss rate and duration, photospheric size etc). The predicted integrated mass loss is in agreement older determinations, of 1-2Msun of ejecta (e.g., Davidson & Humphreys 1997), while the terminal velocity is consistently predicted as well.
Recent observations of η-Car reveal a larger than previously estimated amount of ejected mass (Smith et al. 2003). If the inferred ejected mass is indeed as high as 10 Msun it could indicate that the clumps in the continuum driven winds have a power law scaling law. This was shown by Owocki et al. (2004) to lead a modified mass loss luminosity relation, with larger mass loss rates: $$ \dot{M} = {{W(\Gamma) L_\mathrm{Edd} (\Gamma - 1)^p \over c v_s} } $$ where the power p is related to the power law αp in the truncated distribution of “clump” optical depths: $$ \tau {d f \over d \tau} = {1 \over \Gamma [\alpha_p]} \left( \tau \over \tau_0 \right)^{\alpha_p} e^{-(\tau/\tau_0)} $$ with p = min(1, αp ). It can better explain the larger mass loss rates from η-Car.

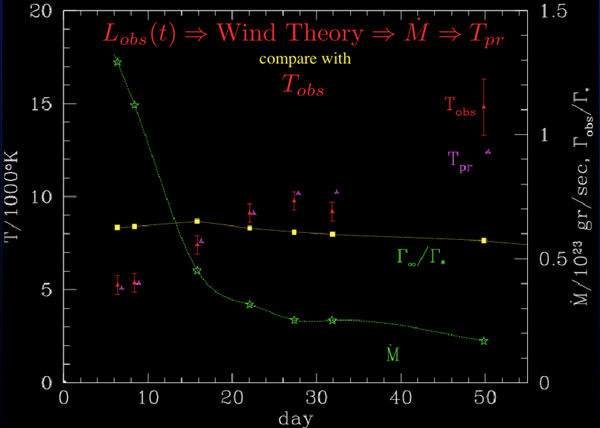
Wind Theory Success: Comparison between the predicted and observed photospheric temperatures as a function of time for nova FH Serpentis. The observed luminosity is used to predict the mass loss rate using the super-Eddington wind loss formula. This in turn is used to predict the location of the photosphere and thus the predicted photospheric temperature Tpr. This predicted temperature can be compared with the observed temperature Tobs. A nice fit is obtained.
References
- Arons, J. 1992. Photon bubbles - Overstability in a magnetized atmosphere. ApJ, 388, 561–578.
- Begelman, M. C. 2002. Super-Eddington Fluxes from Thin Accretion Disks? ApJ, 568, L97–L100.
- Blaes, O., & Socrates, A. 2003. Local Radiative Hydrodynamic and Magnetohydrody- namic Instabilities in Optically Thick Media. ApJ, 596, 509–537.
- Davidson, K., & Humphreys, R. M. 1997. Eta Carinae and Its Environment. ARA&A, 35, 1–32.
- Gammie, C. F. 1998. Photon bubbles in accretion discs. MNRAS, 297, 929–935.
- Glatzel, W. 1994. On the origin of strange modes and the mechanism of related insta- bilities. MNRAS, 271, 66.
- Joss, P. C., Salpeter, E. E., & Ostriker, J. P. 1973. On the ”critical Luminosity” in Stellar Interiors and Stellar Surface Boundary Conditions. ApJ, 181, 429–438.
- Owocki, S. P., Gayley, K. G., & Shaviv, N. J. 2004. A Porosity-Length Formalism for Photon-Tiring-Limited Mass Loss from Stars above the Eddington Limit. ApJ, 616, 525.
- Paczynski, B. 1970. Evolution of Single Stars. I. Stellar Evolution from Main Sequence to White Dwarf or Carbon Ignition. Acta Astronomica, 20, 47.
- Papaloizou, J. C. B., Alberts, F., Pringle, J. E., & Savonije, G. J. 1997. On the nature of strange modes in massive stars. MNRAS, 284, 821–829.
- Shaviv, N. J. 1998. The Eddington Luminosity Limit for Multiphased Media. ApJ, 494, L193.
- Shaviv, N. J. 2000. The Porous Atmosphere of η Carinae. ApJ, 532, L137–L140.
- Shaviv, N. J. 2001a. The Nature of the Radiative Hydrodynamic Instabilities in Radiatively Supported Thomson Atmospheres. ApJ, 549, 1093–1110.
- Shaviv, N. J. 2001b. The theory of steady-state super-Eddington winds and its application to novae. MNRAS, 326, 126–146.
- Shaviv, N. J. 2002. Classical Novae as Super-Eddington Objects. Pages 259–265 of: AIP Conf. Proc. 637: Classical Nova Explosions.
- Spiegel, E. 1976, R. Cayrel & M. Steinberg (eds.), in: Physique des Mouvement dans les Atmospheres Stellaires (Paris: CNRS), p. 267
- Spiegel, E. 1976, in: E. Spiegel & J.-P. Zahn (eds.), Problems in Stellar Convection (Berlin: Springer), p. 19
Links:
Back to page 1
Back to Personal Research
Back to Home page
