Bits of Science / Roundup #1
Blog topic:
Space and Planetary news bits
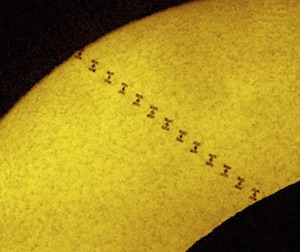
The ISS and moon eclipsing the sun. Uncropped original at www.astrophoto.fr (with many more amazing photos on that site).
You have all heard of (or seen?) the solar eclipse. What you may have missed is that that a few very lucky people actually experienced a double eclipse, partial by the moon and an “annular” eclipse by the international space station. See this image by Thierry Legault.
A friend was surprised that the space station appears so large, but is it?
The space station is at about 400 km (anything lower and its orbit will decay too fast, and anything higher will cost many more of the green stuff). If it has a span of about 100m, it will have an apparent angular size of about $0.1~\mathrm{km}~/~400~{\mathrm km} \approx 1/4000~rad \approx 1’$ (about 1 arc minute, see google units). Given that the diameter of the moon or sun is about 30’, the sizes in the image are reasonable.
• Oceans on Ganymede

Aurorae on Ganymede (credit NASA/ESA).
The magnetic field around Ganymede has two components, one is its own generated (or probably relic) magnetic field, which is fixed to its rest frame. The second component is Jupiter’s magnetic field, however, unlike the first component, this one varies in a frame of reference fixed to Ganymede. Moreover, the location of the auroral ovals depend on the total field. However, because the total field varies, the aurorae are predicted to shift by 5.8° ± 1.3°. In reality, however, the measured variations had an extent of 2.2°±1.3°, Saur et al. used this to infer the existence of an ocean. How come?
Well, a liquid ocean would be conductive (all it requires is just a small amount of salts), which would make the moon a big inductor if present. However, when you try to increase the magnetic field through an inductor, according to Lenz’s law, it will generate a magnetic field that will try to counteract the original magnetic field. The result is a smaller net magnetic field, and hence, the much smaller variation in the auroral oval!
Interestingly, Lentz’s law also implies that the interaction between the induced currents and the generated field produce a force countering the motion. A neat example is this video:
It means that Ganymede has a VERY small “magnetic drag force” operating on it.
Astrophysics news bits:
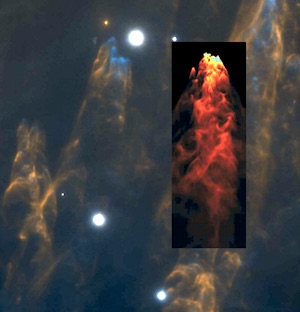
Supersonic moving debris from an explosion that took place 500 years ago. The inset is the result of a simulation. How can the dense blobs be accelerated without being torn apart?
This is already about a month old, but I learned about it only last week, which is why I’m sharing. It appears that in the region of the Orion Nebula (on the “sword of Orion”), there is evidence for a very strange explosive event that took place about 500 years ago. The observations show dozens of what appears to be dense gas blobs moving super-sonically, withe their backwards trajectory emanating from a single point at a single instant. Their typical velocity is 300 km/sec (which is the typical escape speed from stars). This is very high velocity shrapnel!
It really seems strange that it is possible to accelerate such dense gas blobs to such high velocities without disrupting them. But apparently it is possible. The image on the right shows the actual appearance of a few such blobs with the supersonic wake behind them. The inset picture is the result of a simulation, showing that typical Mach numbers of a 1000 are needed to reproduce the observations. You can read more about the observations and the simulations here.
• Supernova kaleidoscope

Supersonic moving debris from an explosion that took place 500 years ago. The inset is the result of a simulation. How can the dense blobs be accelerated without being torn apart?
We can estimate the typical time delay between the images. Since the redshift of the lens is 0.54, it means that the typical distance to it is about half the age of the universe times the speed of light, or about $d = 5 \times 10^{9}$ light years. The perpendicular direction is of order the distance times the angle in radians. Since the separation between the lens and image it of order 1 arc-second, the real distance is about $r = 5 \times 10^{9} / 57/3600 \approx 25000$ light years (57 is the ratio between 1 radian and 1 deg, while 3600 is the ratio between one degree and one arc second).
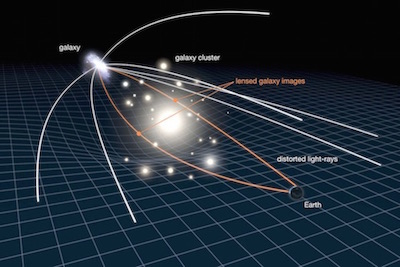
Gravitational lensing implies that light can reach the observer through several paths traversed (source universe today). Each path may have a different duration, thus the images of the supernova should be delayed relative to each other.
The time delay from the extra path is roughly $$ \sqrt{d^2 + r^2} -d \approx { r^2 \over 2 d} \approx 0.06 \mathrm{~light~years~}\approx 3 \mathrm{~light~weeks}. $$ Thus, we expect the typical shifts to be a few weeks. Since SNe last longer than that, it is not surprising that one can see several images at the same time.
