Modeling the COVID-19 / Coronavirus pandemic – 3.The effects of several populations
The next interesting question to ask is what is the effect of a mixed population which has different infection rates. That is, that some individuals are more infectious than others (e.g., a cashier in the supermarket vs. a farmer). For simplicity, we return back to the simpler case where there is no latent period. Let us supposed we have $n$ population that can interact between (i.e., infect) themselves. The equations describing their temporal behavior will then be
\begin{eqnarray}
{d I_1 \over dt} &=& \beta_{11} I_1 + \beta_{12} I_2 + \ldots + \beta_{1n} I_n - \gamma I_1 \nonumber \\
{d I_2 \over dt} &=& \beta_{21} I_1 + \beta_{22} I_2 + \ldots + \beta_{2n} I_n- \gamma I_2 \nonumber \\
&\vdots & \nonumber \\
{d I_n \over dt} &=& \beta_{n1} I_1 + \beta_{n2} I_2 + \ldots + \beta_{nn} I_n- \gamma I_n
\end{eqnarray}
If we now guess exponential behavior for the solution, namely, $I_i \propto \exp(r t)$, we get
\begin{equation}
\newcommand{\matr}[1]{\mathbf{#1}}
(\gamma - r) \matr{I} - \boldsymbol\beta = 0,
\end{equation}
which of course means that $r - \gamma$ are a the eigenvalues of the interaction (infection coefficient) matrix $\boldsymbol\beta$.
This boils down to what are the eigenvalues of random matrices. The easiest way to study their behavior is simply to run "experiments".
As a sanity check, the first case to consider is case for which the infection coefficients are constant. This implies taking the simple case we studied above and partition the population. This should not change anything. Suppose they are equally sized. In such a case, $\beta_{ij} = \beta_0 /n$. The eigenvalues one obtains numerically are $n-1$ zeros, and one $\beta_0$, as expected.
For the next cases, we can consider $\beta{ij}$'s that are random. Since the $\beta{ij}$ have to be positive (no one can "uninfect" an infected patient), we can look at a log normal distribution.
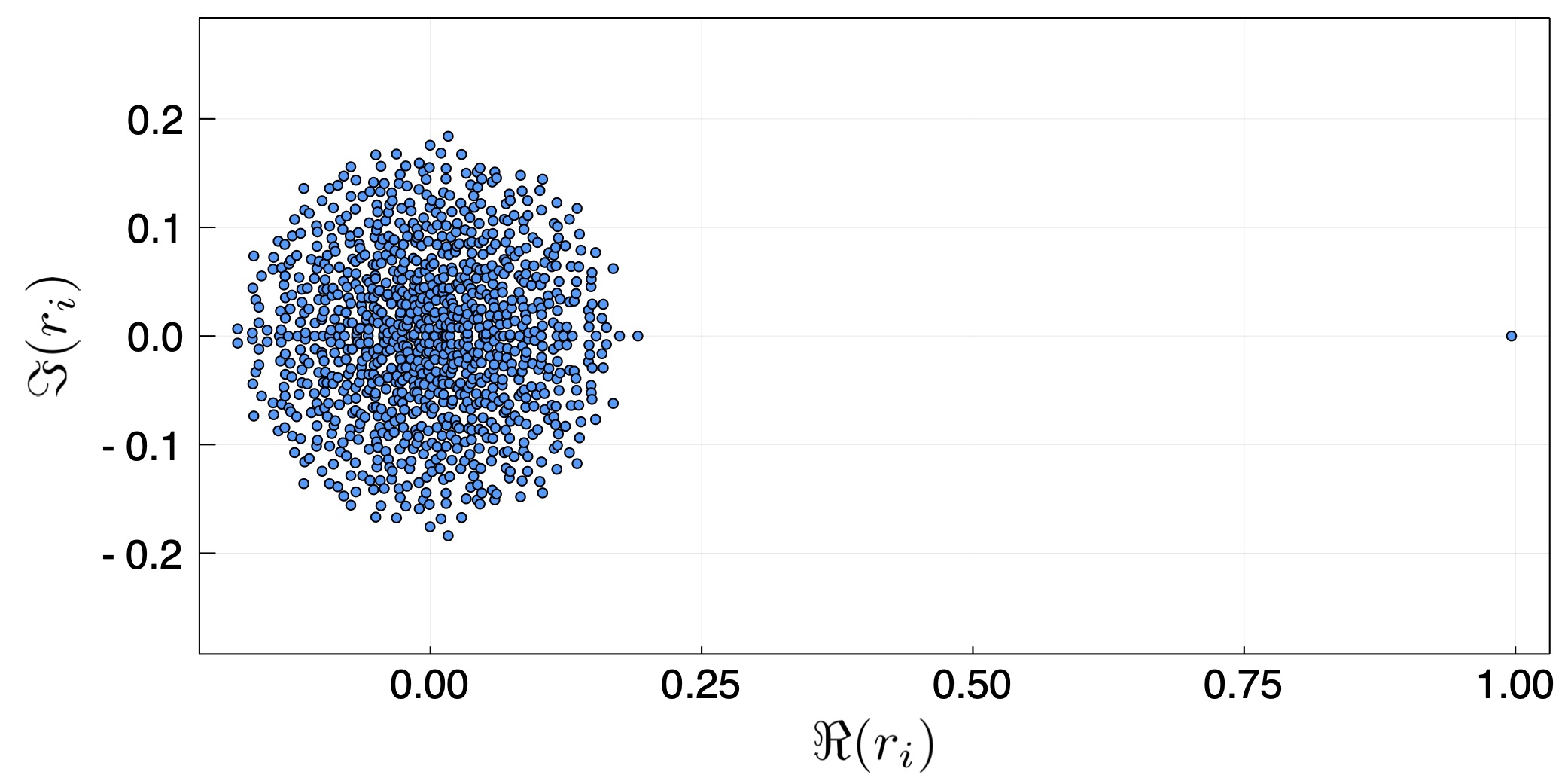
The first random case we take is of a general, non-symmetric matrix. In principle, there is no reason why the coefficients should be symmetric, that is, $\beta_{ij}=\beta_{ji}$. This is because when two people interact, the probability that one will infect the other is not necessarily the same, either because of different habits (one washes her hands while another doesn't), or because of asymmetric interaction (e.g., person providing food vs. a person eating it). Fig. 1 depicts the eigenvalues of a 1000 by 1000 interaction matrix $\boldsymbol\beta$. We see that all but one eigen value fill a circle around the origin, while one eigenvalue is unity. In fact, under some realizations, it can be larger than unity.
The first interesting take away point is that even if the interactions are random, the average interaction sets the maximal growth rate, and it will dominate the solution very early in the evolution. Namely, the initial conditions will cause an oscillatory behavior (because the eigenvalues have an imaginary component), however after a few e-folds at most, the largest eigenmode having an eigenvalue of unity (as the average was normalized), will dominate the growth. Without normalization, we will have $r_{max} = n \overline{\beta_{ij}}$
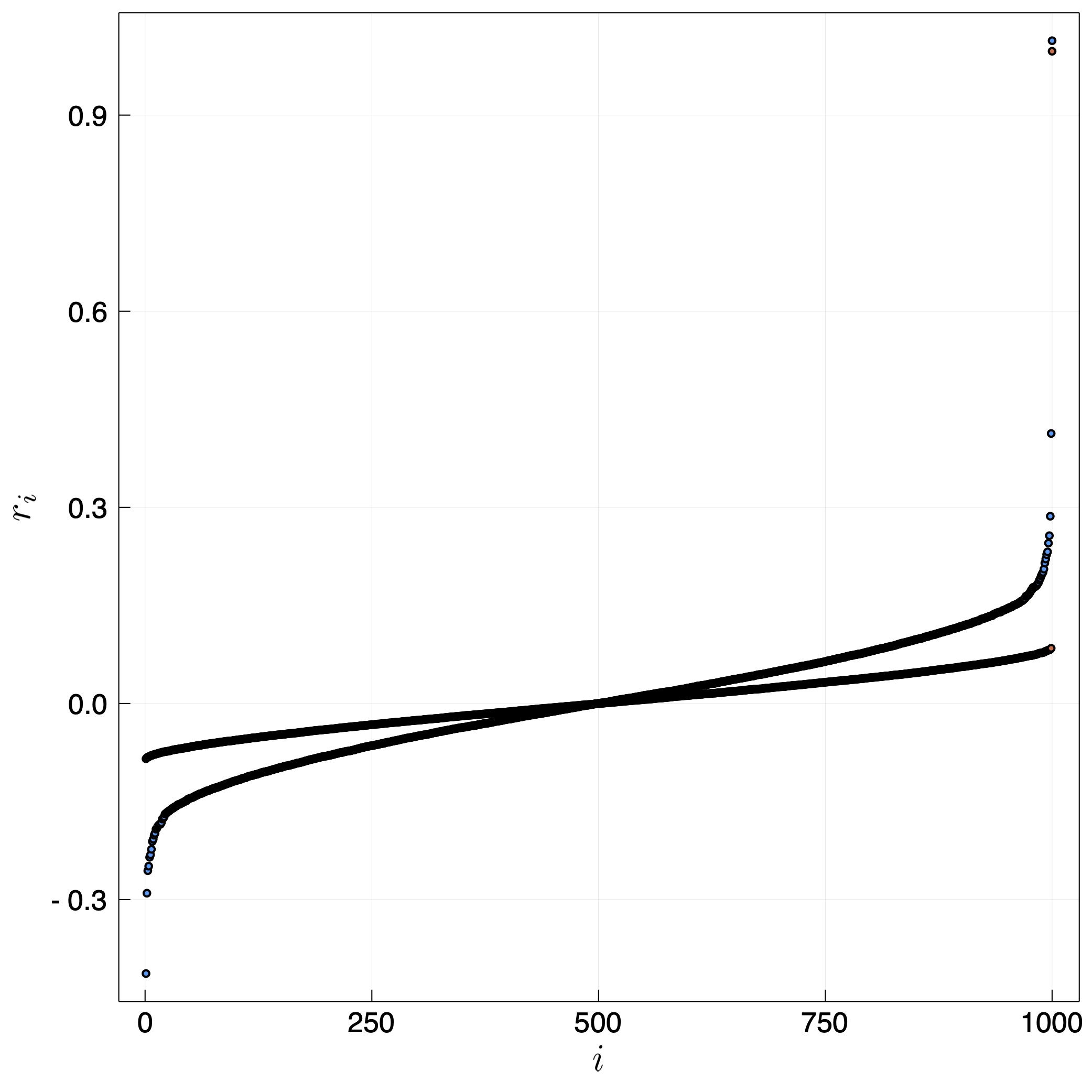
The second random case is considering a symmetric $\boldsymbol\beta$ which will give rise to real eigenvalues (in epidemiological terms, it means that there is symmetric probability that person A and B infect each other if one is sick.
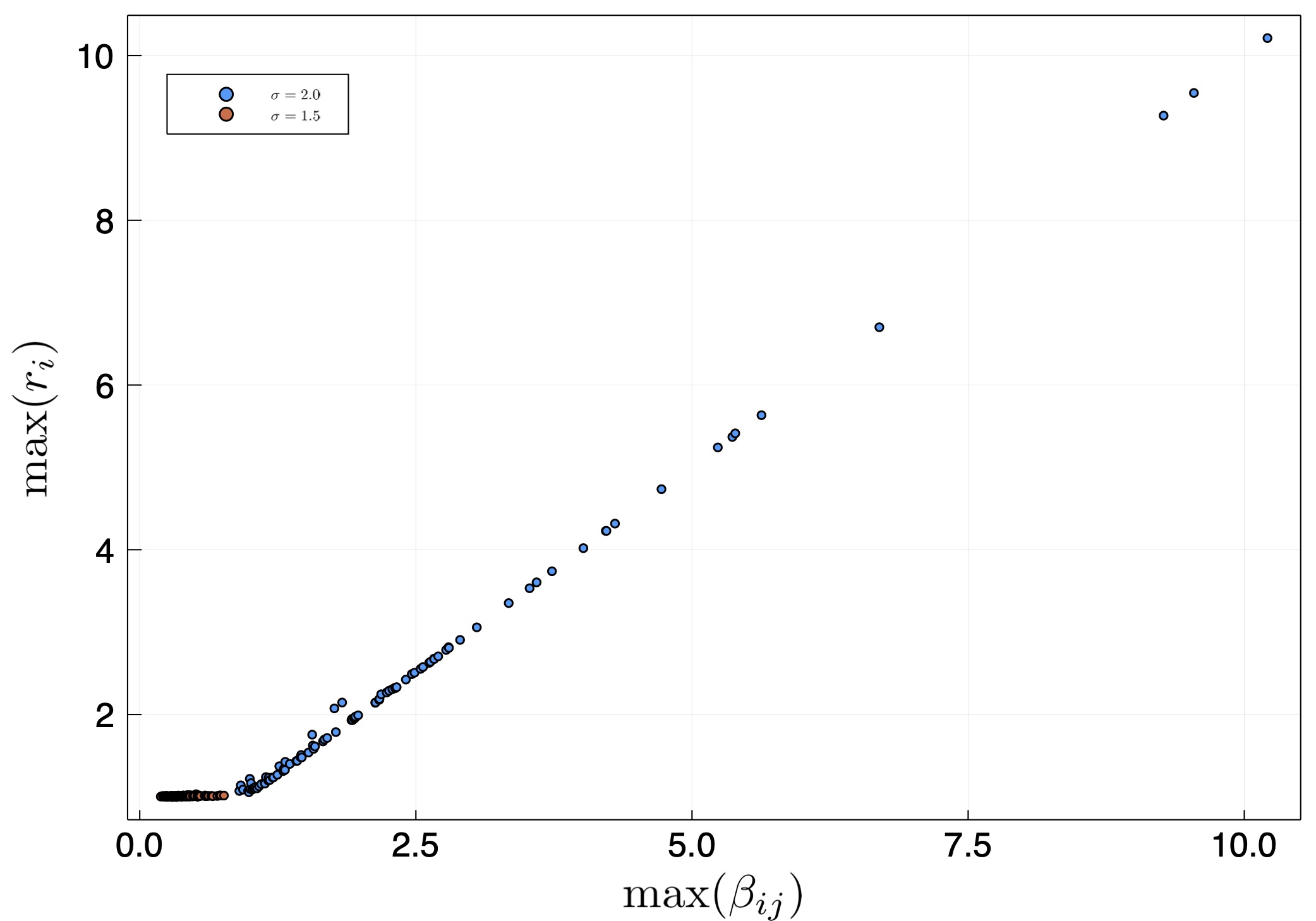
The most interesting aspect is that in some realizations we find that the largest eigenvalue can be larger than unity. We therefore plot in fig. 3 the largest eigenvalue in many random realizations. We find that if the largest element in $\beta_{ij}$ is larger than unity, then the largest eigenvalue is roughly the largest element. Otherwise, it is unity. Interestingly, the distribution width doesn't change this, it only changes the probability that there will be a realization with a very large $\beta_{ij}$.
This result implies that the internal interaction is not critical unless there is a super-spreader, which is someone or some group that has a probability of infecting which is larger than the reciprocal of its size in the relevant population. For example. Suppose a town has 1000 people and 10 delivery guys. If the probability that a single delivery guy will infect someone is larger than the probability that a random person will infect another random person, by a factor which is larger than 100, then the growth exponent will be larger than the exponent that is obtained from the average infection coefficient. It will correspond to delivery guys infecting average people who infect other delivery guys, etc.
Additional posts in the series include
As a sanity check, the first case to consider is case for which the infection coefficients are constant. This implies taking the simple case we studied above and partition the population. This should not change anything. Suppose they are equally sized. In such a case, $\beta_{ij} = \beta_0 /n$. The eigenvalues one obtains numerically are $n-1$ zeros, and one $\beta_0$, as expected.
For the next cases, we can consider $\beta{ij}$'s that are random. Since the $\beta{ij}$ have to be positive (no one can "uninfect" an infected patient), we can look at a log normal distribution.
The first random case we take is of a general, non-symmetric matrix. In principle, there is no reason why the coefficients should be symmetric, that is, $\beta_{ij}=\beta_{ji}$. This is because when two people interact, the probability that one will infect the other is not necessarily the same, either because of different habits (one washes her hands while another doesn't), or because of asymmetric interaction (e.g., person providing food vs. a person eating it). Fig. 1 depicts the eigenvalues of a 1000 by 1000 interaction matrix $\boldsymbol\beta$. We see that all but one eigen value fill a circle around the origin, while one eigenvalue is unity. In fact, under some realizations, it can be larger than unity.
The first interesting take away point is that even if the interactions are random, the average interaction sets the maximal growth rate, and it will dominate the solution very early in the evolution. Namely, the initial conditions will cause an oscillatory behavior (because the eigenvalues have an imaginary component), however after a few e-folds at most, the largest eigenmode having an eigenvalue of unity (as the average was normalized), will dominate the growth. Without normalization, we will have $r_{max} = n \overline{\beta_{ij}}$

Figure 1 - The 1000 eigenvalues of a random 1000$\times$1000 matrix with random elements having a log-normal distribution, normalized to have an average of 1/1000. The width is $\sigma = 2.0$. Evidently, almost all the eigenvalues are in a circle in the complex plane, around the origin. One eigenvalue is unity and real.
The second random case is considering a symmetric $\boldsymbol\beta$ which will give rise to real eigenvalues (in epidemiological terms, it means that there is symmetric probability that person A and B infect each other if one is sick.

Figure 2 - The sorted 1000 eigenvalues of two random 1000$\times$1000 matrix with random elements having a log-normal distribution, normalized to have an average of 1/1000. The width is $\sigma = 1.5$ for the blue points and $1.0$ for the red. We can see that wider distributions of coefficients $\beta_{ij}$ give a wider distribution of eigenvalues around 0. However, for the wider distribution we also find that the largest eigenvalues can be larger than unity.
The most interesting aspect is that in some realizations we find that the largest eigenvalue can be larger than unity. We therefore plot in fig. 3 the largest eigenvalue in many random realizations. We find that if the largest element in $\beta_{ij}$ is larger than unity, then the largest eigenvalue is roughly the largest element. Otherwise, it is unity. Interestingly, the distribution width doesn't change this, it only changes the probability that there will be a realization with a very large $\beta_{ij}$.

Figure 3 - The largest eigenvalue as a function of the largest interaction element $\beta_{ij}$ for many realizations of random matrices having different log-normal distributions.
This result implies that the internal interaction is not critical unless there is a super-spreader, which is someone or some group that has a probability of infecting which is larger than the reciprocal of its size in the relevant population. For example. Suppose a town has 1000 people and 10 delivery guys. If the probability that a single delivery guy will infect someone is larger than the probability that a random person will infect another random person, by a factor which is larger than 100, then the growth exponent will be larger than the exponent that is obtained from the average infection coefficient. It will correspond to delivery guys infecting average people who infect other delivery guys, etc.
Additional posts in the series include
- Background data
- Simple Modeling
- Effects of several populations with a variable infection rate (this page)
- Modeling with at time variable infection rate
- Numerical Model (coming soon!)
- Discussion and Conclusions (coming soon!)
