Many physical systems have a tendency to equilibrate the energy between different components. Sometimes it is exact, and sometimes not. This can arise from a plethora of different reasons, such as equilibrium between forces (which are the derivatives of different energies), equilibrium between reactions (which change energy from one type of energy to another) and of course statistical equilibrium.
One such example are acoustic waves. In them, half the energy is on average kinetic (motion of the gas) and half internal (pressure). Here the equipartition is exact because the waves are exact harmonic oscillations. The interstellar medium is another example. Here, equipartition is only approximate—there is roughly the same energy in the different components, such as internal energy, turbulent energy, magnetic field and energy of the cosmic rays.
With respect to equipartition, stars are no different. In the sun, there is roughly the same binding energy (which is negative) as there is thermal energy. This can also be shown using the
virial theorem. In white dwarfs, the thermal energy is unimportant, instead, it is the
degeneracy energy of the electrons which is expected to be comparable to the gravitational binding energy. We can use this tendency for equipartition to estimate different stellar parameters, such as the
internal temperature of the sun or the
Chandrasekhar mass limit of
white dwarfs.
Conditions at the Center of the Sun
The gravitational binding energy of a test mass $m$ in the gravitational potential outside a mass $M$ is given by:
$$ |E_{grav}| = {G M m \over R} .$$
In case of the binding energy of a star, such as the sun, the test mass is the mass itself, $m \sim M \sim M_{\star}$, such that
$$ |E_{grav}| \sim {G M_\star^2 \over R_\star} .$$
Of course, an astute reader will immediately cry "Oh my goodness!" to the sight of this approximation. Just to remind, however, we are carrying out an order of magnitude exercise. In reality, the integrals should be properly integrated if we are to find an exact result. The binding energy, for example, should actually look like:
$$ |E_{grav}| = \int_{m=0}^{m=M_\star} {G M dm \over r(m)} .$$
The integral will simply introduce a numerical factor of order unity before the $GM^2/R$ expression.
Next, we need to estimate the thermal energy. It is approximately given by:
$$ E_{thermal} = N k T = {M_\star k T \over m_p} .$$
where
N is the number of atoms in the star (of course, and exact calculation should include 3/2 for a monoatomic gas, another factor 2 from the ionized electrons, etc., but we ignore all that in our order of magnitude calculation). $m_p$ is the proton mass (the star is made mostly of Hydrogen).
Equipartition states:
$$ E_{thermal} \sim |E_{grav}| ~~\Rightarrow ~~ T \sim {G M_\star m_p \over k R_\star} .$$
If we plug in the natural constants:
$$G = 6.67 \times 10^{-8} cm^3 gr^{-1} sec^{-2},~~k = 1.38\times 10^{-16} erg/^\circ{\mathrm K},~~m_p = 1.67\times 10^{-24} gr$$
and solar parameters,
$$M_\odot = 2\times 10^{33} gr,~~R_\odot = 7 \times 10^{10} cm. $$
we find a typical temperature of
$$T \sim 2.3 \times 10^{7} {}^\circ{\mathrm K}.$$
This should be compared with $T_{center} \approx 1.5 \times 10^{7}{}^\circ{\mathrm K}$, the actual temperature in the sun. Thus, we estimate a temperature not that far from reality!
The typical radius of a White Dwarf
Using equipartition, we can easily estimate the typical radius of a White Dwarf. Here, the gravitational binding energy (calculated above) is of order the degeneracy energy.
How to we estimate the degeneracy energy? We do so using Heisenberg's uncertainty principle which can be used to estimate the density of quantum states. Heisenberg's principle implies that the uncertainty in the determination of the location and momentum of a particle, is given by:
$$ \Delta x ~\Delta p \sim \hbar .$$
If the density is $n$ (number per unit volume), then each electron is essentially confined to a cube of $\Delta x^3 \approx 1/n.$ This implies that the typical momentum of an electron is: $ p \sim {\hbar / \Delta x} \sim {\hbar n^{1/3}}$. The energy of a typical electron will therefore be:
$$ E_1 \sim {p^2 \over 2 m_e} \sim {\hbar^2 n^{2/3} \over m_e} $$
(after dropping factors of 2, which we don't need since the calculation is an inaccurate estimate only). This energy is of order the Fermi energy. If the star has a total of $N_e$ electrons, then the total degeneracy energy of the star will be of order:
$$ E_{deg} \sim N_e E_1 \sim {\hbar^2 n^{2/3} N_e\over m_e} $$
Moreover, the total number of electrons in the star is $N_e = M_\star Z / A m_p$, where
A is the atomic mass (number of nucleons per atom) while
Z is the number of electrons per atom. We can also write $n = N_e/V \sim N_e/R_\star^3$. We thus find:
$$ E_{deg} \sim {\hbar^2 \beta^{5/3}\over m_e m_p^{5/3}} M_\star^{5/3} R_\star^{-2} , $$
where
β≡Z/A.
Next, we can use energy equipartition to estimate the equilibrium. That is, we assume that the gravitational binding energy is of order the degeneracy energy. Hence,
$$E_{deg} \sim |E_{grav}| ~~~\Rightarrow ~~~ {\hbar^2 \beta^{5/3}\over m_e m_p^{5/3}} M_\star^{5/3} R_\star^{-2} \sim {G M_\star^2 \over R_\star} $$
After minor algebraic manipulation, we find:
$$ R_\star \sim {\hbar^2 \beta^{5/3} \over G m_e m_p^{5/3}} M_{\star}^{-1/3} = 2 \times 10^4 \left(\beta \over 0.5\right)^{5/3} \left(M \over M_\odot\right)^{-1/3} km$$
Note that we write the result with $\beta = 0.5$ since it is the typical value found in white dwarfs. To obtain the exact value of the prefactor, the actual equation of state and hydrostatic equations have to be integrated over. Interestingly, it is one of the few cases where this can be done almost analytically, since white dwarfs (with non-relativistic electrons) are nearly
polytropic. The real value of the prefactor obtained through an honest to god solution is about 9000 km, i.e., about a factor of 2 discrepancy. However, the approximation does properly capture the different dependencies (e.g., on mass). Not bad for a very rough approximation!
Relativistic Electrons and the Chandrasekhar Mass Limit
We assumed above that the electrons are non-relativistic. However, if the radius of the star becomes small enough, the Fermi energy would increase sufficiently to become comparable to the electron rest mass, and even surpass it. Let us look at the equilibrium obtained if we assume that the electrons are relativistic.
If we assume that the electrons are relativistic, then the energy of a typical electron will now be:
$$ E_1 \sim {p c} \sim {\hbar n^{1/3} c}. $$
The total degeneracy energy of the star is:
$$ E_{deg} \sim N_e E_1 \sim {\hbar n^{1/3} c N_e} \sim {\hbar M_\star^{4/3} \beta^{4/3} c \over R_\star m_p^{4/3}}$$
Again, we compare this energy to the gravitational binding energy and obtain:
$$E_{deg} \sim |E_{grav}| ~~~\Rightarrow ~~~ {\hbar M_\star^{4/3} \beta^{4/3} c \over R_\star m_p^{4/3}} \sim {G M_\star^2 \over R_\star} $$
This time, the radius of the star cancels out! We find a typical mass which is:
$$ M_{Ch} \sim \left( \hbar \beta^{4/3} c \over G m_p^{4/3} \right)^{3/2} \approx 1.8 \beta^2 M_\odot $$
The more exact value obtain from the actual solution of the problem is
$$ M_{Ch} \approx 5.87 \beta^2 M_\odot $$
That is, with the approximation, we were only a factor of 3 off.
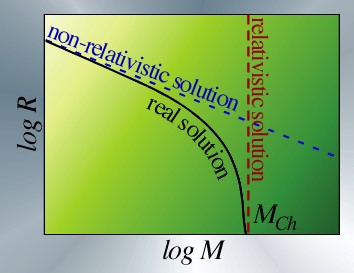
The mass-radius relationship of white dwarfs. For low masses, the solution is that obtained by non-relativistic degenerate electrons. As the mass is increased, the relativistic solution is approached. There is no solution above the Chandrasekhar Mass Limit.
Essentially, we see that once white dwarfs become compact enough for the electrons to be relativistic, there is a solution with only one mass, irrespective of the radius. What does this mean?
If we take a non-relativistic white dwarf, as we increase it's mass, its radius will become smaller and smaller, scaling as $M_\star^{-1/3}$. As the white dwarf approaches the Chandrasekhar mass limit $M_{Ch}$, the electrons become more and more relativistic, and the slope must become sharper than -1/3. The obtained Mass-Radius relationship of white dwarfs can be seen in the figure.
Once the white dwarf surpasses $M_{Ch}$, there is no solution. This basically implies that irrespective of how much we compress the star, the pressure by the relativistic electrons could never balance the pull of gravity, and the object would simply collapse until something else could withstand the pull of gravity. This is the degeneracy pressure of neutrons, and the object formed is therefore called a neutron star.
Comments (2)
The above is very nice.
But why is the sun mass equal to the Chandrasekhar mass?
There should be a simple dimensional argument. And at present I cannot figure it out.
I would understand the equality of the two masses if the temperature at the center of the sun equals the temperature when electrons become relativisitic. But this is wrong by a factor 500.
So the connection should be more subtle.
I think it is a coincidence that the typical mass of stars is similar to the Chandrasekhar mass. Another interesting coincidence is that the mass for which stars become radiation pressure dominated is also similar (well, an order of magnitude larger). Why? I don't know... I think it is a coincidence between the two different mass combinations of the constants of nature.